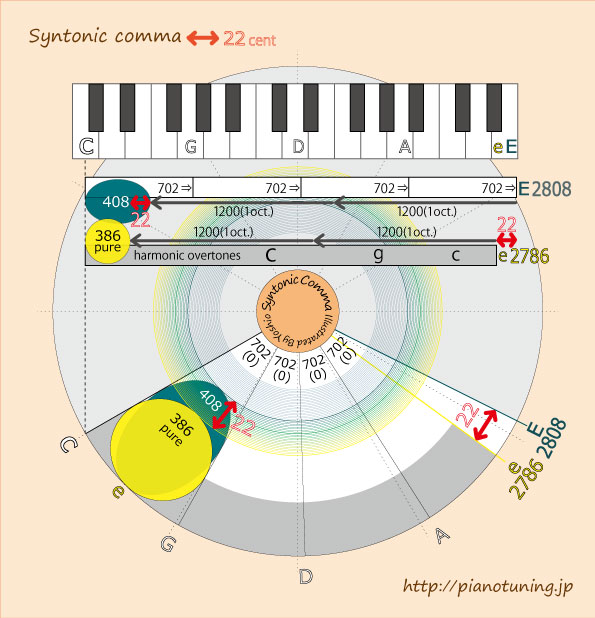
Syntonic comma
C (基音)の音が鳴っている時、小さいエネルギーですが、e(第五倍音)の自然倍音が鳴っています。
この音程のeなら他でもう一つ鳴らしても完全にとけ合います。このCとeの音程差は2786cent。
一方、C→G→D→A→E と 純正五度を4回積み重ねるとEの音ができます。
このCとEの音程差は、702×4=2808cent。
この音程の差(2808-2786=22cent)をシントニックコンマと呼んでいます。
このEの音は、C の自然倍音の eと比べると22centも高い音となり、Eとeを同時に鳴らすと、たくさんの唸りが生じます。
五度の音程は、ぴったり合った音程にしたいけれど、 4つの純正五度を積み重ねると、高いEの音ができてしまうのです。
鍵盤楽器で唸りのない長三度[純正三度]を作るためには、二つの方法が試みられています。
一つは「キルンベルガーⅠ」に見られる、「純正律」を使う方法で、主要三和音の[F-C C-G G-D]を純正五度[702cent]にして、D-Aだけで22centを受け持たせています。もう一つ、「ミーントーン」の手法では、隣り合う4つの五度で22centを均等[22÷4=5.5]に受け持ち、それぞれを(702cent-5.5cent=) 696.5centにしています。但し、この696.5centの五度が濁っている事や、C → G と弾いた時、Gの音程が低く感じることは否めません。
純正三度を得るためにシントニックコンマ[22cent]を分け合う考え方は、ピタゴラスコンマ[24cent]を分け合う考え方と「対比的なコンセプト」となるのも面白いところです。
http://okamotopiano.jp 岡本ピアノ工房 岡本芳雄