『ピタゴラスコンマ』（音律に内在する歪み：その1）
※Cを起点として作図しています

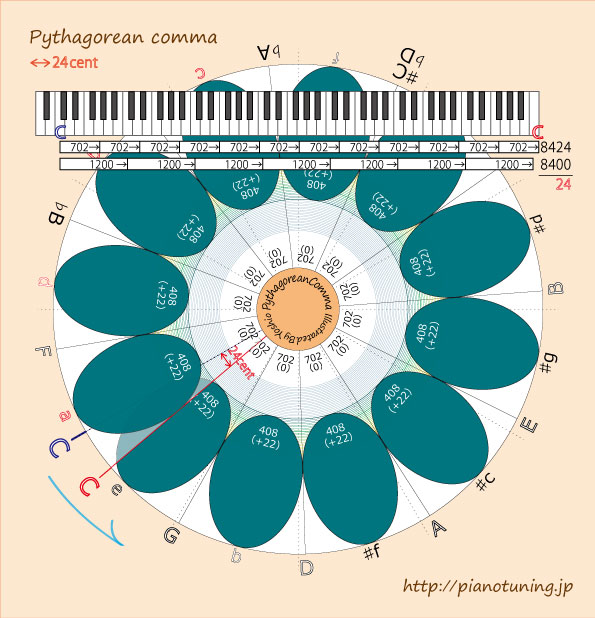
C→G→D→A→E→B→♯F→♯C→♯G→♯D→♯A→F→ C
C から五度を積み重ねていくと、12回目に再び C がやってきます。
♪純正五度を12回重ねた音⇒　702cent×12=8424cent
♪７オクターブ上の音⇒　1200cent×7=8400cent

C は、元の音C の7オクターブ上より、24cent（半音の約1/4）高いと言うことになるのです。

この2つの音の音程差[8424-8400=24cent] を ピタゴラスコンマ（Pythagorean comma）と呼んでいます。

図：C から純正五度を次々に足していくと、元の Cを通り過ぎたところにC ができてしまいます。

鍵盤楽器で、2つの音程のCを作るわけにはいかないので、様々な五度の配列を工夫して円環を綴じています。
この+24centを12コの五度で等しく分け合う(24÷12= 2cent) と、平均律に。
6コで等しく分け合い(24÷6=4cent) 白鍵のほうで受け持つと、ヴァロッティやヤングⅡに。
など、いろいろな方法でつじつま合わせをしているのです。

ピタゴラスコンマ[24cent] を分け合う考え方は、シントニックコンマ(三度の音程差)[22cent]を分け合う考え方と「対比的なコンセプト」になるのも面白いところです。

注：このときに出来ていく長三度の音程は、ピタゴラスの三度と呼ばれる唸りの多い408cent。図では、純正五度をいつまでも重ねて行った場合を仮想して作図しています。

http://okamotopiano.jp　岡本ピアノ工房　岡本芳雄